Алгебра 7 класс
Линейные уравнения.Линейные неравенства.
Тест "Решение задач с помощью линейных уравнений"
Степень с натуральным показателем.
Свойства степени с натуральным показателем
Степень с целым показателем
Таблица степеней
Стандартный вид числа
Запомните!Источник: http://math-prosto.ru
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
a · 10n,
где 1 ≤ a < 10 и n — натуральное число.
где 1 ≤ a < 10 и n — натуральное число.
Такая запись называется — стандартный вид числа.
При этом число «n» называют порядком числа «a».
При этом число «n» называют порядком числа «a».
Из определения выше важно понять, что степень, в которой стоит «10», в стандартном виде числа называется порядком.
Теперь к примеру. Пусть нам дано число «5 600» и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».
В числе «5 600» первая цифра справа — «5». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.
Значит, чтобы из «5,600» получить «5600» нам нужно умножить «5,600» на «1000». Запишем полученное преобразование.
Значит, чтобы из «5,600» получить «5600» нам нужно умножить «5,600» на «1000». Запишем полученное преобразование.
5 600 = 5,600 · 1000
Теперь запишем «1000» с использованием степени.
5 600 = 5,600 · 1000 = 5,600 · 103
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
5 600 = 5,600 · 1000 = 5,600 · 103 = 5,6 · 103
Таким образом «5 600» в стандартном виде будет выглядеть следующим образом:
5 600 = 5,6 · 103
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
5,6 · 103 = 5 600
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь «0,017».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от «1» до «9».
В десятичной дроби «0,017» вначале идет «0». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от «0».
Это цифра «1». Посчитаем сколько знаков (цифр) стояло от запятой до цифры «1», включая саму цифру «1».
Получается два знака. Начнем записывать «0,017» в стандартном виде. Перенесем запятую и поставим ее справа от «1».
Получается два знака. Начнем записывать «0,017» в стандартном виде. Перенесем запятую и поставим ее справа от «1».
0,017 = 1,7 · 10…
Ответим себе на вопрос: "На что нужно умножить или разделить «1,7», чтобы получить изначальное число «0,017» ?". Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится влево.
Выходит, чтобы из «1,7» сделать 0,017», нужно «1,7 разделить на «100» (чтобы перенести запятую на два знака влево).
0,017 = 1,7 : 100
Запишем это деление на «100», используя обыкновенную дробь.
0,017 = 1,7 : 100 = 1,7 ·
| 1 |
| 100 |
С помощью отрицательной степени запишем окончательный вид числа «0,017» в стандартном виде.
0,017 = 1,7 : 100 = 1,7 ·
= 1,7 · 10−2
| 1 |
| 100 |
Выражения и их преобразования
Одночлены
Часто при решении задач мы используем буквенные множители и числа вместе.
Выражение 5a2b — это произведение трёх множителей: 5a2b = 5 · a2 · b. Подобные произведения буквенных и числовых множителей называют одночленами.
Запомните!
Произведение числовых и буквенных множителей называют одночленом. Примеры одночленов: ac, 2xy2, −7xy, 0,5a3b.
Из чего состоит одночлен
Числовой множитель, который есть в одночлене, принято называть коэффициентом одночлена. Буквенные множители иногда называют переменными.
Если в одночлене явно нет числового коэффициента, значит числовой коэффициент одночлена равен 1.
Например, для одночлена ab — числовой коэффициент равен 1. Это связано с тем, что при умножении на 1 одночлен остаётся прежним, поэтому коэфффицент 1 не записывают перед одночленом.
1 · a · b = ab
1 · a · b = ab
Также не записывают явно коэффициент «−1». Вместо этого ставят знак «−» перед одночленом. При такой записи все понимают, что коэффициент одночлена равен «−1». Например, у одночлена «−xyz» коэффициент равен «−1».
Приведение одночлена к стандартному видуЗапомните!
Одночлен, у которого единственный числовой множитель стоит на первом месте и буквенные множители в различных степенях не повторяются, называется одночленом стандартного вида. Буквенные множители следует располагать в алфавитном порядке.
Примеры одночленов стандартного вида: 2at, 16y3, −17pxy, 3d4
Примеры одночленов нестандартного вида: 2acа,
4xy2 · 3, x4y · (−7).
Не забывайте, что одночлен — это произведение числовых и буквенных множителей, поэтому внутри одночлена действуют все законы умножения, в том числе переместительный закон умножения.
Чтобы привести одночлен к стандартному виду нужно сделать следующее.
Важно!
Пример. Привести к стандартному виду одночлен 3ada · 8.
- Перемножаем все числовые коэффициенты
3 · a · d · a · 8 = 3 · 8 · a · d · a = 24 · a · d · a - Теперь, используя свойства степени, перемножаем все буквенные множители.
24 · a · d · a = 24 · a · a · d = 24a2d - Что такое степень одночлена
Запомните!
Степень одночлена — это сумма всех степеней буквенных множителей.
Например, степень одночлена 9a2b равна 3, т.к. у a2 (вторая степень), у b (первая степень): 2 + 1 = 3.Число «0» (ноль) называется нулевым одночленом. Степень нулевого одночлена не определена.Но не путайте с одночленом нулевой степени! Одночлен нулевой степени — это любое число (например, 123; 0,5; −324).Любое число можно записать как произведение числа на буквенный множитель в нулевой степени. Т.е. 123 = 123 · a0 = 123 · 1 = 123 (одночлен нулевой степени).Одночлен нулевой степени получил свое название, потому что любой буквенный множитель можно представить как 1 через нулевую степень. - Вначале, необходимо понять, что называют подобными одночленами.
Запомните! - Одночлены, у которых одинаковый состав букв и их степеней, называют подобными.
Одночлены нужно рассматривать как единое целое.То есть, частая ошибка когда, например, одночлены 3a и 2ab считают подобными, т.к. в обоих одночленах присутствует буквенный множитель а.Одночлены 3a и 2ab НЕ являются подобными, потому что состав букв должен полностью совпадать в обоих одночленах.В данном примере в одночлене 3а из буквенных множителей только а, а во втором одночлене 2ab — два буквенных множителя а и b.Запомните!
Складывать и вычитать можно только подобные одночлены. Как складывать и вычитать одночлены
- При сложении и вычитании одночленов работаем только с их числовыми коэффициентами. Состав букв остается всегда прежним!Разберем пример: 3a2b + 2a2b
- 1.Сначала убедимся, что данные одночлены подобные.
У первого одночлена 3a2b состав букв со степенями: a2b.
У второго одночлена 2a2b состав букв со степенями: a2b.
- 1.Сначала убедимся, что данные одночлены подобные.
- Состав букв и их степеней у обоих одночленов одинаков, значит, одночлены подобные и их можно складывать.
- 2.Теперь рассмотрим числовые коэффициенты одночленов.
У первого одночлена 3a2b коэффициент: 3.
У второго одночлена 2a2b коэффициент: 2. - 3.Сложим их коэффициенты: 3 + 2 = 5
- 4.Запишем окончательный ответ в виде суммы одночленов.
3a2b + 2a2b = 5a2b
Еще раз обратите внимание, что состав букв в итоговом одночлене НЕ поменялся.Запомните!
3a2b + 2a2b = 5a2b
Противоположные одночлены взаимно уничтожаются.
−73x2z + 73x2z = 0
Примеры сложения и вычитания одночленов
- 1)7x2y − 2x2y = 5x2y
- 2)2a3 + 3a3 − a3 = 5a3 − a3 = 5a3 − 1 a3=
- = 4a3
- 3) ab3 + ab3 = 1ab3 + 1ab3 = 2ab3
- 4) 5t − 6t = −t (т.к. 5 − 6 = −1)
- 5) 8xy − 10xy + 2xy = −2xy + 2xy = 0
- (т.к. при вычитании коэффициентов −2 + 2 = 0)
Запомните! - 2.Теперь рассмотрим числовые коэффициенты одночленов.
- При умножении одночленов числа умножаются с числами, а буквы с буквами.
Как умножать одночлены
- В первую очередь перемножаются числовые коэффициенты.Так как в любом одночлене между числовым коэффициентом и буквенными множителями стоит знак умножения, можно воспользоваться переместительным законом умножения.Рассмотрим пример: 3ab · 2a2c3ab · 2a2c = 3 · a · b · 2 · a2 · с =
- 3 · 2 · a · a2 · b · с = 6 · a · a2 · b ·сОдинаковые буквенные множители перемножаем по свойствам степени.
6 · a · a2 · b · с = 6 · a1 + 2 · b · с = 6a3bcПри умножении числовых коэффициентов с разными знаками, в первую очередь определяем итоговый знак результата по правилу знаков.
−2ax · (−3x2y) = (−2)·(−3)a · x · x2 · y = 6 · a · x1 + 2 · y = 6ax3yПримеры умножения одночленов
Важно! - Перед умножением одночленов убедитесь, что они приведены к стандартному виду.
- 2t2 · 7t3 = 14t2 + 3 = 14t5
- −5t · 5t3x = −25t3 + 1x = −25t4x
аb2 · 3a3b =1 3
aa3b2b = a1 + 3 b2 + 1 = a4b33 3
Чтобы разделить одночлен на одночлен нужно:
- 1)записать деление одночленов в виде дроби;
- 2)сократить числовые коэффициенты по правилу сокращения дробей;
- 3)сократить буквенные множители по свойству степени.
Запишем деление одночленов в виде дроби. На верх дроби (в числитель) запишем первый одночлен, в низ (в знаменатель) — второй одночлен.
В первую очередь всегда определяйте знак результата и ставьте его перед дробью.
Примеры деления одночлена на одночлен
- b5 : b2 =
= b5 − 2 = b3b5 b2 - (−x2y3z2)2 : xyz =
=(−1 · x2 y3 z2)2 xyz
=(−1)2 x2 · 2 y3 · 2 z2 · 2 xyz
=
= x4 − 1 y6 − 1 z4 − 1 = x3 y5 z31 · x4 y6 z4 xyz
При делении на одночлен, у которого числовой коэффициент представлен в виде обыкновенной дроби, не стоит записывать «многоэтажные» дроби.
Лучше воспользоваться правилом деления обыкновенных дробей и «перевернуть» второй одночлен, заменив деление умножением.
- Запомните!
- При возведении в степень одночлена в степень возводится числовой коэффициент и каждый буквенный множитель.
Рассмотрим пример возведения в куб одночлена: (2a2x)3
Вначале возведем в степень отдельно числовой коэффициент и каждый буквенный множитель.
(2a2x)3 = 23(a2)3 x3
(2a2x)3 = 23(a2)3 x3
При возведении в степень буквенных множителей используем правило
возведения степень в степень.
возведения степень в степень.
Напоминаем, что при возведении степени в степень показатели степеней перемножаются.
23(a2)3 x3 = 23 a2 · 3 x3 = 8a6x3
23(a2)3 x3 = 23 a2 · 3 x3 = 8a6x3
Запишем итоговое решение.
(2a2x)3 = 23(a2)3 x3 = 23a2 · 3x3 = 8a6x3
(2a2x)3 = 23(a2)3 x3 = 23a2 · 3x3 = 8a6x3
Примеры возведения в степень одночленов
- 1)(3а)3 = 33a3 = 27a3
- 2)(−2b)2 = (−2)2b2 = 4b2
- 3)(
x2m4)3 = (1 2
)3 (x2)3 (m4)3 =1 2
x2 · 3 m4 · 3 =13 23
x6m12 (в данном примере используем правило возведения в степень дроби)1 8 - 4)(−ab2)2 = (−1)2a2 b2 · 2 = 1a2 b4 = a2 b4
- 5)(−3px)3 = (−3)3 p3 x3 = −27p3 x3
Что такое многочлен
Часто путают понятия одночлена и многочлена.
Давайте разберемся, что называют одночленом, а что многочленом. Прежде всего, вспомним, что называли одночленом в уроке «Одночлены».
Обратите внимание, что «внутри» одночлена (между буквами и числовым коэффициентом) есть только знак умножения. Например, в одночлене: 3ab = 3 · a · b
- Запомните!
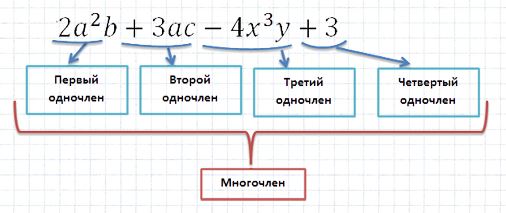
Многочленом называется алгебраическая сумма нескольких одночленов.
Одночлены, из которых составлен многочлен, называют членами многочлена.
Примеры многочленов: a + 2b2 − c; 3t5 − 4b;
4 − 6xy
Несложно заметить, что любой многочлен состоит из нескольких одночленов.
Возникает вопрос, почему многочленом называют алгебраическую сумму одночленов, если в многочлене присутствует знак минуса.
Это объясняется тем, что на самом деле знак «−» относится к числовому коэффициенту одночлена, который стоит справа от знака.
В многочлене знак, который стоит слева от одночлена относится к числовому коэффициенту самого одночлена.
Как найти степень многочлена
- Запомните!
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Степени многочленов
| Многочлен | Степень многочлена | ||||
|---|---|---|---|---|---|
| a2 − 3a2b + x = a2(степень одночлена 2) − 3a2b(степень одночлена 3) + x(степень одночлена 1) | 3 | ||||
| 4 | ||||
| 8x2 − 3a + 4 = 8x2(степень одночлена 2) − 3a(степень одночлена 1) + 4(степень одночлена 0) | 2 |
Любой одночлен является многочленом. В самом деле, любой одночлен, по сути, является многочленом, который состоит всего из одного одночлена.
Примеры таких многочленов: 2a2b; −3d3; a.
Число «0» называют нулевым многочленом.
Стандартный вид многочлена.
Прежде чем приводить многочлен к стандартному виду необходимо вспомнить, что называют подобными одночленами.
Важно!
Подобными одночленами называют одночлены, у которых одинаковый состав букв и их степеней.
Примеры подобных одночленов: ab и 2ab, −3c2d и c2d.
Также вспомните, как привести одночлены к стандартному виду .
После того, как вы освежили знания по этим двум вопросам, вы готовы перейти к приведению многочлена к стандартному виду.
Как привести многочлен к стандартному виду
- Запомните!
Чтобы привести многочлен к стандартному виду, нужно:
- 1)Привести каждый одночлен многочлена к стандартному виду.
- 2)Выполнить приведение подобных одночленов.
Рассмотрим пример. Привести к стандартному виду многочлен:
3ab + 2 · 3с2 + 2ab − 8сс + xy =
3ab + 2 · 3с2 + 2ab − 8сс + xy =
- 1)Вначале приведём к стандартному виду все одночлены внутри многочлена.
3ab + 2 · 3с2 + 2ab − 8сс + xy = - 3ab + 6с2 + 2ab − 8 с1 + 1 + xy =
= 3ab + 6с2 + 2ab − 8с2 + xy
Приведение подобных в многочлене
Помните, что при приведении одночленов складываются и вычитаются только их числовые коэффициенты.
3ab + 6с2 + 2ab − 8с2 + xy = 3ab + 2ab − 8с2 + 6с2 + xy = 5ab −2c2 + xy
3ab + 2 · 3с2 + 2ab − 8сс + xy = 3ab + 6с2 + 2ab − 8 с1 + 1 + xy =
= 3ab + 6с2 + 2ab − 8с2 + xy = 3ab + 2ab − 8с2 + 6с2 + xy = 5ab −2c2 + xy
При раскрытии скобок не забывайте использовать правило знаков. При перемещении одночлена знак слева переносится вместе с ним.
Примеры приведения многочлена к стандартному виду- 5a − 7b − (7a − 5b) = 5a − 7b − 7a + 5b = 5a − 7a − 7b + 5b =
- −2a − 2b
- 11a2 + 7a + 9a2 −5a = 11a2 + 7a + 9a2 − 5a = 11a2 + 9a2 + 7a − 5a = 20a2 + 2a
- 13ab − 0,2xy − 2a · 5b + 6x · 0,2y + a(−3)b = 13ab − 0,2xy − 10ab + 1,2xy + (−3ab) =
- 13ab − 10ab − 3ab − 0,2xy + 1,2xy =
- 0 · ab + 1 · xy = 0 + xy = xy
Иногда приведение подобных в многочлене называют упрощением алгебраического выражения.
Сложение и вычитание многочленов
При сложении и вычитании многочленов важно уметь использовать правила раскрытия скобок.
Рассмотрим два случая раскрытия скобок:
- 1)когда перед скобками стоит знак «+»;
- 2)когда перед скобками стоит знак «−».
Правила раскрытия скобок
- Запомните!
Чтобы раскрыть скобки, перед которыми стоит знак «+», нужно просто опустить скобки.
Все знаки у одночленов внутри сохраняются.
Рассмотрим пример. Раскрыть скобки:
3x2 − 5xy − 7x2y + (5xy − 3x2 + 8x2y) =
3x2 − 5xy − 7x2y + 5xy − 3x2 + 8x2y
- Запомните!
Рассмотрим пример. Раскрыть скобки:
7t3 − 4p − (2t − tn + t) = 7t3 − 4p − 2t + tn − t
Обратите внимание, так как в этом примере перед скобками стоит знак «−», при раскрытии скобок все одночлены поменяли знаки на противоположные.
Как складывать и вычитать многочлены
Чтобы сложить или вычесть многочлены нужно:
- 1)раскрыть скобки по правилам раскрытия скобок;
- 2)максимально привести подобные.
Результат суммы и разности двух многочленов является многочленом.
Рассмотрим пример.Найти разность многочленов:
3a2 + 8a − 4 и 3 + 8a − 5a2
3a2 + 8a − 4 и 3 + 8a − 5a2
- Запишем пример. Не забудем заключить весь второй многочлен в скобки.
3a2 + 8 a − 4 − (3 + 8a − 5a2) = - 3a2 + 8 a − 4 − 3 − 8 a + 5a2
- Теперь подчеркнем и приведем подобные.
3a2 + 8a − 4 − 3− 8a + 5a2 - = 3a2 + 5a2 + 8a − 8a − 4 − 3 = 8a2 − 7
- Запишем окончательное решение.
3a2 + 8 a − 4 − (3 + 8a − 5a2) = - 3a2 + 8a − 4 − 3− 8a + 5a2 =
- 3a2 + 5a2 + 8a − 8a − 4 − 3 = 8a2 − 7
- Источник: http://math-prosto.ru







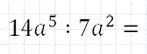







Комментарии
Отправить комментарий