Алгебра 10 класс
Смена 11 (05.11 - 19.11)
Повышенный уровень
Построение графиков с модулем
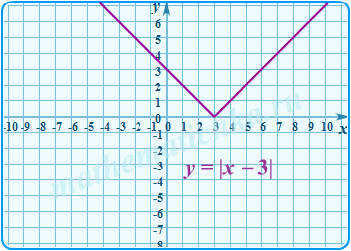
- Построить график функции y = f(x).
- Исключить его часть, расположенную в отрицательной половине оси абсцисс. (Например, просто стереть ластиком, если график был построен карандашом.)
- Построить левую ветвь графика (при отрицательных x) симметричным отображением его правой ветви относительно оси Oy.
- Построить график функции y = f(x).
- Участок графика, расположенный ниже оси абсцисс (при отрицательных y) развернуть на верхнюю половину координатной сетки преобразованием симметрии относительно оси Ox.
Пример 1.
Задан график функции y = x2.
Построить график функции y = |x2 − 2x − 5|
На следующем шаге производим отражение участка графика, расположенного ниже оси Ox в верхнюю половину координатной плоскости. Результат на рисунке.
.
Пример 2.
Построить график функции y = |x + 2| + |x − 1|.
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1|, используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участках, например, при x = −3 и x = 3. На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).
Пример 3.
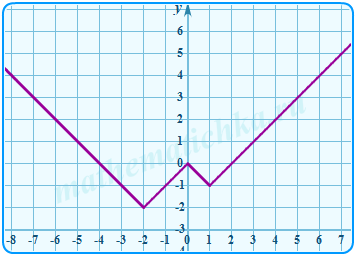
Построить график функции y = |x + 2| + |x − 1| − |x|.
К двум исходным графикам предыдущего примера добавляем график y = −|x|, построенный с помощью отражения на нижнюю координатную полуплоскость.
Имеем 3 разных модуля, следовательно 3 границы, 4 участка и 5 точек, необходимых для построения ломаной. Три точки берём на изломах построенных графиков, 4-ю и 5-ю на крайних участках.
Результат на рисунке.
Деление многочленов
Тригонометрия
Формулы приведения
Преобразование тригонометрических выражений
Тригонометрические уравнения
Производная
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Задача. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
Производная в жизни
Повышенный уровень
ПОВТОРИ
Геометрическая прогрессия
Определение геометрической прогрессии
| bn+1 =bn · q, где bn ≠ 0, q ≠ 0 |
Знаменатель геометрической прогрессии
| |
| Формула n-го члена геометрической прогрессии | bn = b1 · q n-1 |
| Сумма n первых членов геометрической прогрессии | |
| Характеристическое свойство геометрической прогрессии | bn2 = bn-1 · b n+1 |


















Комментарии
Отправить комментарий